나를위한 진동학 정리 1편

 

이전의 네이버 블로그에 있던 글을 이동하고있습니다.
기말고사 대비겸 전공지식을 백업중입니다.
이 포스팅은 공학수학 2nd O.D.E와 고체역학, 동역학, 정역학을 배웠다는 가정하에 쓰여졌습니다.

Vibration(진동)의 기초

Vibration is a mechanical phenomenon whereby oscillationsoccur about an equilibrium point.

평형점에대해 진동하는 기계적인 현상을 진동이라 한다.

그리고 진동은 Potential (V) Energy 와 Kinetic(T) Energy간의 상호작용에서 발생한다.

진동을 배우는 이유는 자연계의 모든 구조물은 정적이지않고 항상 진동하게되어있으며, 진동은 때로 구조물을 파괴하기도합니다.
이를 방지하기위해 자연계의 진동에 관해 공부할 필요가 있습니다.

일반적인 진동 형태, 위 사진은 나중에 알겠지만 Undamped Motion이다.

대표적인 진동의 3가지 요소는 이러합니다.
각각 Inertia, Elasticity, Damping 요소가 있습니다. 각각 설명하자면

1. Inertia element (관성 요소)

관성 요소란 무엇일까? 관성이란 알다싶이 물체가 외부의 힘을 받지 않는 한 정지 또는 운동의 상태를 지속하려고 하는 성질을 의미한다. 그렇다면 실생활의 예를 들어 보았을 때, 관성은 무게와 속도에 비례한다는 사실을 알 수 있다. 자동차가 무거울수록, 자동차가 빠를수록 제동거리가 늘어난다는 것은 당연한 상식이다. 이는 관성에 의한 현상이며, 이를 이 식으로 표현할 수 있다.

$$T=\frac{1}{2}m{v}^2=\frac{1}{2}m{\dot{x}}^2$$

T 는 맨 위에서 말했듯 Kinetic Energy로 운동에너지라한다. 운동에너지는 질량과 속도의 제곱의 비례한다는 사실을 알 수 있다.

이 밖에도 회전운동에대한 식으로도 쓸 수 있는데 이는 아래와 같이 표현할 수 있다.

$$T=\frac{1}{2}J{\dot{\theta }}^2$$
여기서 J는 관성모멘트이고 세타에 점붙어있는 것은 각속도이다. 관성모멘트는 다음과 같이 표현한다.
$$J=\int r^{2}dm$$

관성모멘트는 반지름의 제곱에 비례한다. 예 중 하나는 피겨스케이팅 선수가 팔을 벌리다가 안으로 접었을 때 회전속도가 증가하는 모습을 통해서 이해가 가능하다. 운동에너지(T)는 일정한데 J가 줄어드니 각속도가 증가하는 현상을 보인다.

2. Elasticity element (탄력 요소)

탄력을 가진 대표적인 예로 스프링(Spring)을 들 수 있다. 진동학에서는 이를 Potential Energy(V)로 사용한다. 아래의 식은 각각 직선운동과 회전운동의 Potential Energy를 의미합니다.

$$V=\frac{1}{2}k{x}^2$$
$$V=\frac{1}{2}{k}_t{\theta }^2$$
k란 스프링 상수로 단위는 N/m이고, kT는 회전스프링상수로 N-m/rad단위를 사용합니다.

3. Damping element (감쇠 요소)

Damper란 진동을 방해하여 에너지를 소산(Dissipation)하는 역할을 한다. 점성 감쇠운동에서는 Rayleigh dissipation function이 이렇게 주어진다. 아래의 식은 각각 직선운동과 회전운동을 의미합니다.

$$R=\frac{1}{2}c{\dot{x}}^2$$$$R=\frac{1}{2}c{\dot{\theta }}^2$$

여기서 C는 점성감쇠계수이다. 둘다 같지만 단위가 위의 직선운동은 N-s/m 단위를 쓰고, 회전운동은 m-N-s/rad 단위를

내가 배운 진동은 여러가지가 있지만 3학년때 배울 내용은 4가지가있다.

• Undamped Vibration

진동하는동안 에너지 손실이 전혀 없는 진동이다.

• Damped Vibration

진동하는동안 에너지 손실이 있는 운동을 의미한다.

• Linear Vibration

모든 진동의 시스템 요소들이 선형으로 작용하는 진동을 의미한다.

• Deterministic Vibration

예측가능한 진동을 의미한다.

---

How to solve? 어떻게 풀어야하나

진동을 분석하는데 있어 4단계의 절차가 필요하다.

1. 수학적 모델링

질량이 분포된(Distributed) 시스템이냐, 분리된(Discrete) 시스템이냐 판단합니다.

왜 두가지 방법이 있을까. 첫번째 Distributed 시스템은 현실적이지만 분석하기가 매우 까다롭다. 이는 Partial Differential Equation(편미분방정식)으로 풀어야한다. 그에 비해 두번쨰 Discrete 시스템은 이상적이고, 분석하기쉽지만 의외로 실제의 값과 가깝습니다. 이는 ODE(상미분방정식)으로 풀 수 있습니다.

2. 운동방정식을 유도한다.

뉴턴의 2법칙이나 Energy method(Lagrange’s Equation)을 사용한다.

뉴턴의 2법칙이란 무엇일까? F=ma다. 뉴턴의 2법칙을 이용해서 풀려면 FBD(Free Body Diagram)를 이용해서 풀어야하며, 벡터를 활용한 방법이다. 하지만 이 방식은 시스템이 복잡해질수록(x,y,z축 등 외부의 힘이 추가될경우) 풀기 난해하다. 그에비해 Energy method 방식은 T, V, R 각각 Kinetic E, Potential E, Reyleigh dissipation function을 활용해서 풀고 각각 요소들을 편미분하여 특정식을 도출하여 푸는 방식이다. 이 방법은 처음에는 어려워보이지만, 시스템이 복잡해질수록 간단하다. 그리고 FBD를 사용할 경우 좌표계의 +,-을 맞춰주어야하는데 이 방법은 그럴필요없다. 한마디로 개꿀!

3. 운동방정식을 푼다
4. 결과를 분석한다

---

Degree of Freedom (DOF)

Degree of Freedom(앞으로 DOF)이란 무엇일까? 운동방적식을 표현하는데 있어 필수적이고 독립적인 좌표들의 개수라합니다.

DOF는 좌표계의 개수(The number of coordinates)에서 제약조건(The number of constraints)을 뺀것의 숫자와 동일합니다.

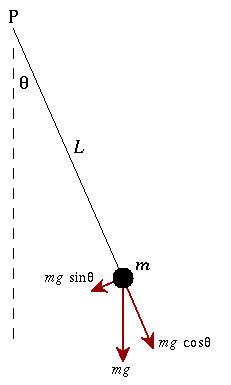
위 시스템의 DOF을 알아보자. 기본적으로 이런 운동은 x,y축의 운동으로 표현할 수 있습니다.
그렇다면 좌표계의 개수는 2개! 그리고 제약조건은 무엇일까? 답은 바로 L 이다. L은 m의 좌표 (x,y)의 제곱에 루트를 씌운 값과 동일한데 이것이 바로 제약조건입니다.

그래서 2-1=1 바로 1개! 그 1개는 바로 (𝛉)이다.

Generalized Coordinates

Generalized Coordiantes란 무엇일까?

이의 정의는 독립된 좌표계의 집합으로 DOF의 개수와 동일합니다.

위의 사진에서 보면 M을 (x1,y1)으로 표현할 수 있고, m을 (x2,y2)로 표현할 수 있으며 제약조건은 L과 l로 두개이다. 그렇다면 4-2 = 2로 DOF는 2이며, 그 두개는 (𝛼,β)입니다.

Frequency, Period

Frequency(주파수) 란 주기적인 운동이다. 조화운동은 Circular Frequency이다. 이는 sin함수 혹은 cos함수의 운동을 한다. 사실 둘다 동일하다. sin(𝛉-𝝅/2) 는 cos(𝛉)랑 같으니말이다.

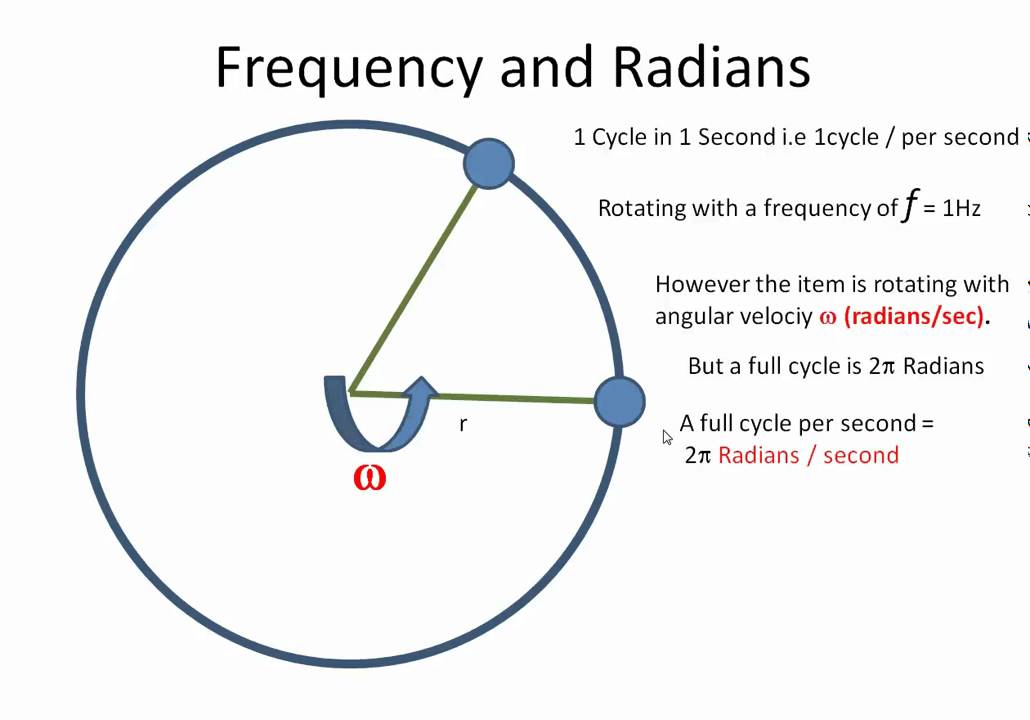
좌표축에서 최고지점까지의 거리를 Amplitude라하고, 최고점에서 최고점사이의 거리를 Period라 한다. Period 는 주기이며, 주기는 다음과 같이 표기할 수 있습니다.

$$T=\frac{2\pi }{\omega }$$

단위는 second 즉 초이다. 당연하다 주기 말그대로 시간이다. 그리고 frequency는 다음과 같이 계산한다. 주기의 역수가 주파수이다. 주파수의 단위는 Hz입니다.

$$f=\frac{1}{T}$$

Spring Mass Model

Spring-Mass 모델에 작용하는 중력을 알아보자.
보통 Spring-Mass모델은 이렇게 생겼다.

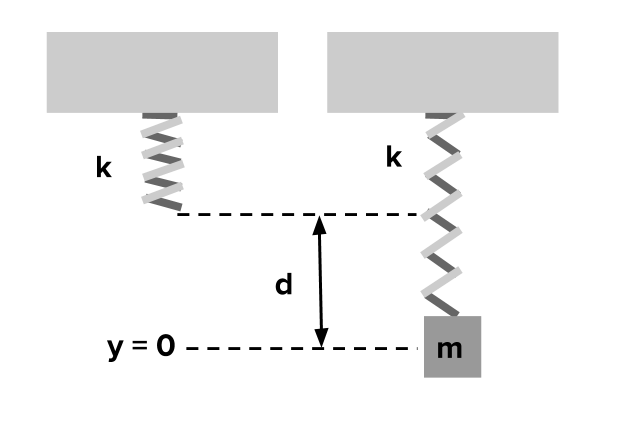
k는 위에서 말했듯 스프링상수이고 d는 Static Deformation이다. y=0인 지점은 Equilibrium position 즉 평형점이다. 에너지 보존 법칙을 이용하면 다음과 같이 표기할 수 있다.

$$\sum F_x=0=-kd+mg$$

이 방정식은 정적인(Static) 경우에 해당한다. 방향은 아랫방향을 +값으로 잡았다. 그러면 동적인(Dynamic) 경우는 어떨까?

$$\begin{gathered} \sum F_x=m\ddot{y}=-k(d+y)+mg \\ kd-mg=0 \\ \therefore m\ddot{y}+ky=0 \end{gathered}$$
보통 y좌표계를 안쓰고 x를 쓰지만 사진이 y라서 y로표현하였다. 위 식에서 맨 아래의 식이 동적인(Dynamic)경우의 Equation of motion이다.

위 식을 보면 kd-mg로인해 중력이 사라지는 멋진 식을 볼 수 있다.

즉 이 운동에서는 중력이 관여하지 않는다.

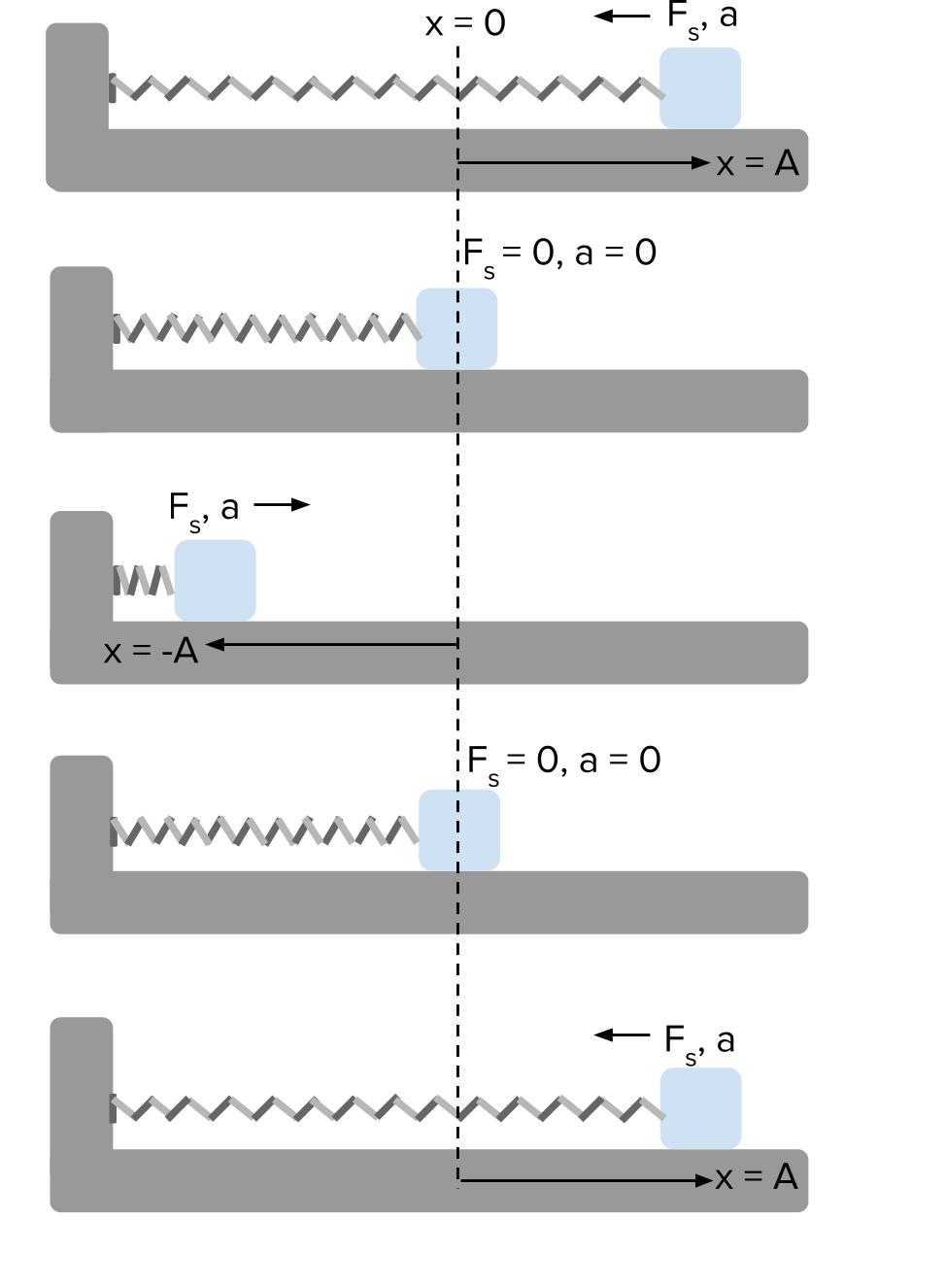
그러면 이런 운동은 어떻게 풀어야할까? 가운데 점선은 Equilibrium position이고 스프링상수는 k, 물체의 질량은 m, 초기 변위는 x0라 하자. 그리고 지면과 물체간의 작용하는 friction(마찰)은 무시한다. 이를 뉴턴의 2법칙을 활용한 방정식 말고 Lagrange’s Equation으로 구현이 가능하다.

$$\frac{d}{dt}(\frac{\partial T}{\partial {\dot{q}}_k})-(\frac{\partial T}{\partial q_k})+(\frac{\partial V}{\partial q_k})=Q_k$$

Lagrange equation을 정리하면 기존의 운동방정식과 똑같은 식이 나온다. 그렇다는 것은 뉴턴의 2법칙으로 푸는 방법보다, Lagrange equation으로 푸는게 간단하다는 이야기가 된다.

오늘은 여기까지 쓰고. 다음장부터는 좀 더 깊숙하게 들어가보겠습니다.

Written with StackEdit.