
기본 작동 원리
대표적인 고전 제어시스템으로 PID 컨트롤러가 있다. PID는 (Proportional-Integral-Derivative)의 약자로 P, I, D Term에 error e(t)가 곱해져 출력이 나오는 형태이다.
Setpoint = r(t)
Measured Process Variable (PV) = y(t)
Error = e(t) = r(t) - y(t)
Control Variable = u(t)
Term P
P항은 e(t)에 비례한 값에 곱해져서 제어하고자 하는 대상의 System Input이 되는 항이다.
e(t)가 커진다면 P항은 마찬가지로 증가하게 된다. 이런 특성으로 인해 P항을 Gain 으로 칭하고 “K”로 부른다.
P항만 있어도 제어하고자 하는 대상의 Output을 얻을 수 있다. 하지만 P항만을 이용해서는 원하는 목표값으로 도달하는것이 불가능하다.
Term I
I항은 SP-PV 즉 e(t)값을 누적한 값(적분값)에 해당한다. 이를 통해서 얻을 수 있는 것은 목표값에 도달할 때 Error을 완전히 없앨 수 있다.
단점이 있다면 누적된 값으로 인해 Integral Effect가 생겨 Overshoot이 생길 수 있다.
Term D
D항은 SP-PV 즉 e(t)를 미분하여 기울기를 알아내어 미래의 값을 예측하는 항목이다.
e(t)의 변화율에 대응할 수 있는 항목이다.
Control Action
Control Variable(Action) u(t)는 0-100% 같이 표현된다. e(t)의 값이 양수라면 output의 값도 증가하는 방향성을 보인다.
Error 증가 ⇒ Control Output 증가
Error 감소 ⇒ Control Output 감소
수학적 표현
PID 컨트롤러를 시간축에서 표현하면 다음과 같다.
$$ u(t) = K_p e(t) + K_i \int^{t}_{0} e(\tau)d\tau + K_d \frac {de(t)} {dt} $$
PID컨트롤러를 Laplace Transform으로 표현하면 다음과 같다.
$$ u(s) = (K_P + K_I \frac {1} {s} + K_D s) e(s) $$
$K_p,K_i,K_d$는 모두 음수가 아닌 항목이다. 일반적인 경우 $K_i, K_d$는 $\frac {K_p} {T_i}, K_pT_d$로 각각 표현한다.
$T_i$는 Integration Time Constants로 얼만큼의 시간동안 error을 누적할지를 결정하고
$T_d$는 Derivative Time Constants로 Set Point에 도달하기 위한 미분값을 결정하는 상수이다.
$$ u(t) = MV(t)=K_p e(t) + K_i \int^{t}_{0} e(\tau)d\tau + K_d \frac {de(t)} {dt} $$
u(t)는 Manipulated Variable로 PID의 output에 해당한다. 이 중 I항에는 $\tau$로 표기되어있는 것을 볼 수 있는데 0~t초까지 적분할 값을 나타내는 것이기 때문이다.
PID 컨트롤러를 Laplace Transform하면 다음과 같이 표현이 가능하다.
$$ L(s) = K_P + K_I \frac {1} {s} + K_D s $$
Proportional Term
P항 즉 Proportional Term은 Output을 e(t)에 비례해서 Output을 생성해준다.
Proportional 항목으로부터 나오는 Output은 다음과 같이 정의 가능하다.
$$ P_{out} = K_pe(t) $$
P항목이 증가할수록 주어진 Error에 대해서 추종하는 경향성이 커진다.
하지만 너무 증가한다면 전체적인 시스템이 불안정한 경향성을 띄우고, 너무 낮다면 시스템이 원하는 목표치에 도달하지 못하고, Disturbance에 대해서 불안정성이 커진다.
그로인해 최적의 P값을 찾는 과정이 필요한데 이를 Loop Tuning(Shaping)이라 한다.
Steady-state Error (SSE)
Steady state error는 안정되었을 때의 error값 즉 목표값과 실제값의 차이값을 의미한다.
Proportional Controller는 Process Gain(K)(System의 Gain)에 비례하고 Controller의 Gain에 반비례하는 관계를 가지고 있다.
Integral Term
I항이 Controller의 영향을 주는것은 error값과 error의 지속시간이다.
Integral 항목은 일정 시간의 error을 누적하여 Controller output에 적용하여 SSE를 0으로 만들어 주는 역할을 한다.
I항은 Integral Gain($K_i$) 에 곱해져서 Controller Output에 적용된다. I항목의 Output은 다음과 같이 표현할 수 있다.
$$ I_{out} = K_i\int^t_0e(\tau)d\tau $$
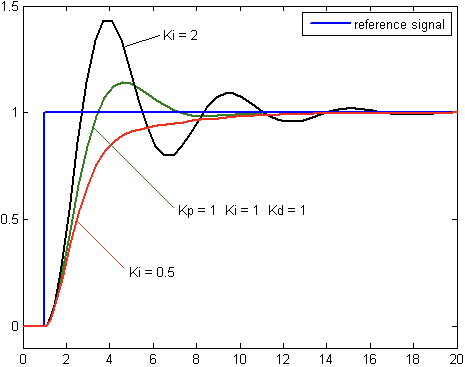
위의 그림을 보면 $K_i$가 적용되었을 때 SSE를 0으로 만들어주는 모습을 볼 수 있다.
하지만 Integral Term이 증가할수록 과거의 오류 누적값이 쌓여 Overshoot이 생기는 것을 확인할 수 있다.
이러한 Overshoot을 개선하기 위해서 필요한 것이 Loop Tuning 이다.
Derivative Term
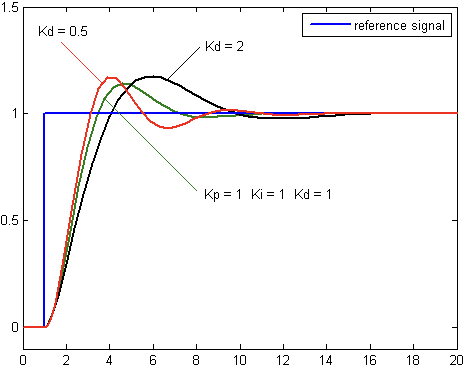
D항은 Error의 Slope 즉 Rate of Change에 영향을 주는 항목이다.
$$ D_{out} = K_d\frac {de(t)} {dt} $$

D항은 시스템의 경향을 예측하여 Settling Time과 시스템의 안정성을 개선한다.
일반적인 경우, D항목을 사용하기 위해서는 Low-pass Filter을 거쳐서 D항을 생성하게 된다. 이는 시스템이 고주파 혹은 노이즈에대해서 제한을 걸어 시스템의 불안정성을 개선한다.
'제어공학 (Control Theory)' 카테고리의 다른 글
| 시스템 판별이란? (System Identification) (0) | 2022.11.29 |
|---|---|
| Bode Plot, Margin에 대하여 (0) | 2022.11.29 |
| 제어공학 간단 소개글 (0) | 2022.11.29 |
| 제어 시스템의 종류 (0) | 2020.05.02 |