Bode Plot은 Linear Time Invariance (LTI) 시스템의 주파수 응답 특성을 그리는 그래프 중 하나이다.
Bode Plot에 나타낼 것은 바로 Frequency에 따른 Magnitude와 Phase이다

x축 ⇒ log frequency scale 즉 주파수를 log scale로 표현
y축 ⇒ Magnitude(크기)는 단위가 dB이며, 아래 그래프의 Phase(위상)의 단위는 degree이다.
상단의 그래프를 Magnitude Plot으로 명칭하는데, 주파수 평면 상에서 시스템의 크기를 의미한다.
하단의 그래프는 Phase Plot으로 Phase Shift을 의미한다.
dB란..?
$$ 20log_{10}\frac {V_{out}} {V_{in}} $$
입출력의 비(Transfer Function 을 설명했던 것과 똑같다)에 20log을 취한 것이 dB(데시벨)의 정의이다.
다음은 많이 쓰이는 dB값이다.
$$ 3dB = 20log_{10}\sqrt{2}\\-3dB = 20log_{10}\frac{1}{\sqrt{2}}\\10dB = 20log_{10}\sqrt{10}\\20dB = 20log_{10}10 $$
-3dB는 Magnitude가 0.7배로 감소한 것을 의미한다.
1차 극점 (Pole)
시스템의 특성 방정식으로 표현된 상태의 분모에 근을 하나 가지는 경우
$$ H(s) = \frac {a} {s+a} $$
와 같이 표현 가능하며 그래프로 표현시 다음과 같이 표현이 가능하다.
Magnitude Plot

현 시스템은 다음과 같은 특성을 가진다.
💡 Breakpoint : $\omega = a$
Low Frequency. asymptote (점근선) : 0dB
High Frequency. asymptote : -20dB/decade
Actual curve is -3dB below breakpoint
$\omega = a$ 일때 시스템의 Magnitude 는 -3dB정도로 감소하면서 그 후로 -20dB씩 감소한다.
Phase Plot
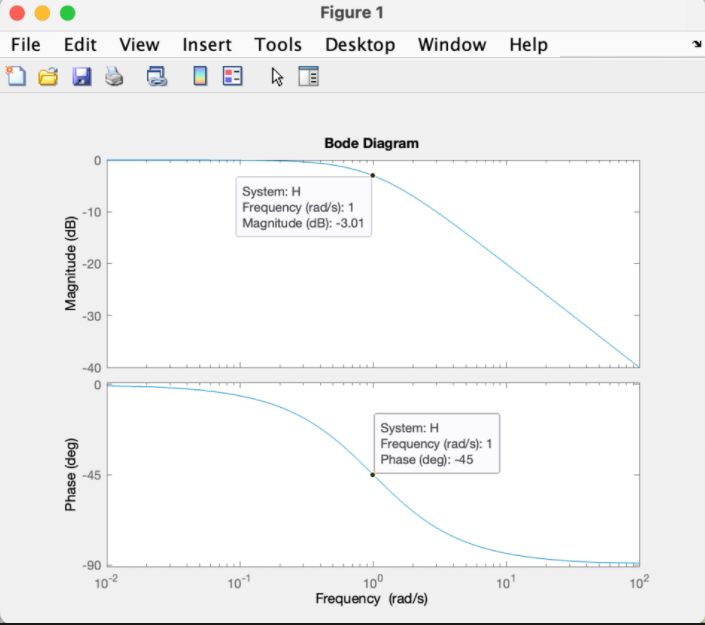
💡 Low Frequency. asymptote ⇒ $0\degree$
$45\degree$ at breakpoint $\omega = a$
High Frequency. asymptote : $-90\degree$
$0\degree$ at $\omega \approx \frac {a} {5}$, $-90\degree$ at $\omega \approx 5a$,
break point에서 -45도 지점을 지나며, phase 0에서 시작해 -90에서 마무리 된다.
1차 시스템의 Zero(영점)
a = 1인 시스템을 가정하였다.
$$ H(s) = \frac {s+1} {1} $$

Zero(영점)의 Bode Plot을 보면 break point $\omega = 1$ 지점에서 3dB씩 증가하는 것을 볼 수 있다.
💡 Breakpoint : 1
Low Frequency. asymptote (점근선) : 0dB
High Frequency. asymptote : 20dB/decade
Actual curve is 3dB below breakpoint
💡 Low Frequency (점근선) ⇒ $0\degree$
$45\degree$ at breakpoint $\omega = a$
High Frequency. (점근선) : $90\degree$
$0\degree$ at $\omega \approx \frac {a} {5}$, $90\degree$ at $\omega \approx 5a$,
Second Order system ⇒ 2 poles
2차 시스템은 다음과 같이 표현 가능하다 (표준 표현)
$$ H(s) = \frac {\omega_n^2} {s^2 + 2\zeta\omega_ns+\omega_n^2} $$
2차 시스템의 Magnitude 와 Phase 는 다음과 같이 표현 가능하다.

Frequency 별로 Magnitude 차트는 다음과 같이 표현되게 된다.

2차 시스템은 Resonance(공진)하는 곳의 변화가 $\zeta$에 따라 다르게 나타난다.
위 그림을 보고 다음과 같은 결과를 도출할 수 있다.
💡 Low Frequency ⇒ 0dB
High Frequency ⇒ -40dB/decade
Breakpoint ⇒ $\omega = \omega_n$
Resonant peak = $\frac {1} {2\zeta}$
Actual Max of magnitude ⇒ $(2\zeta\sqrt{1-\zeta^2})^{-1}$ at $\omega = \omega_n\sqrt{1-2\zeta^2}$
Break Point을 지나고 고주파로 들어설수록 -40dB/decade 로 Magnitude가 감소한다.
Phase의 경우 다음과 같다.
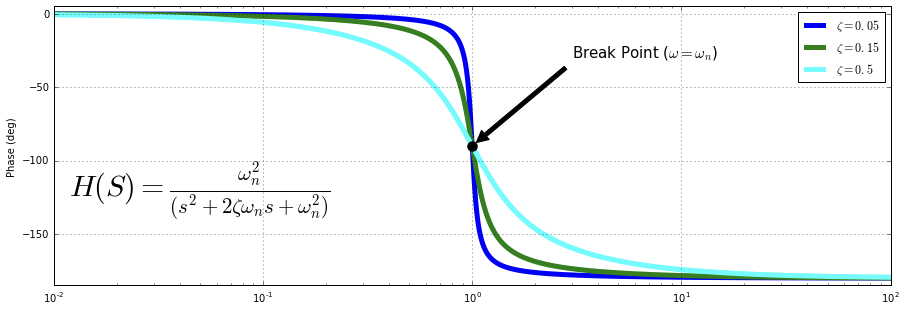
💡 Low Frequency ⇒ $0\degree$
High Frequency ⇒ $-180\degree$
$-90\degree$ at breakpoint $\omega = \omega_n$
Slope closes $0\degree$ at $\omega \approx \frac {\omega_n} {5^{\zeta}}$, $-180\degree$ at $\omega \approx \omega_n5^{\zeta}$,
zeta가 작을수록 가파른 모양을 가지게 된다.
Cutoff Frequency
Margin
지금까지 Bode Plot을 알아본 것은 Gain Margin과 Phase Margin을 알아내기 위함이다. 그렇다면 Bode Plot을 보고 어떻게 Gain Margin과 Phase Margin을 알아낼까?
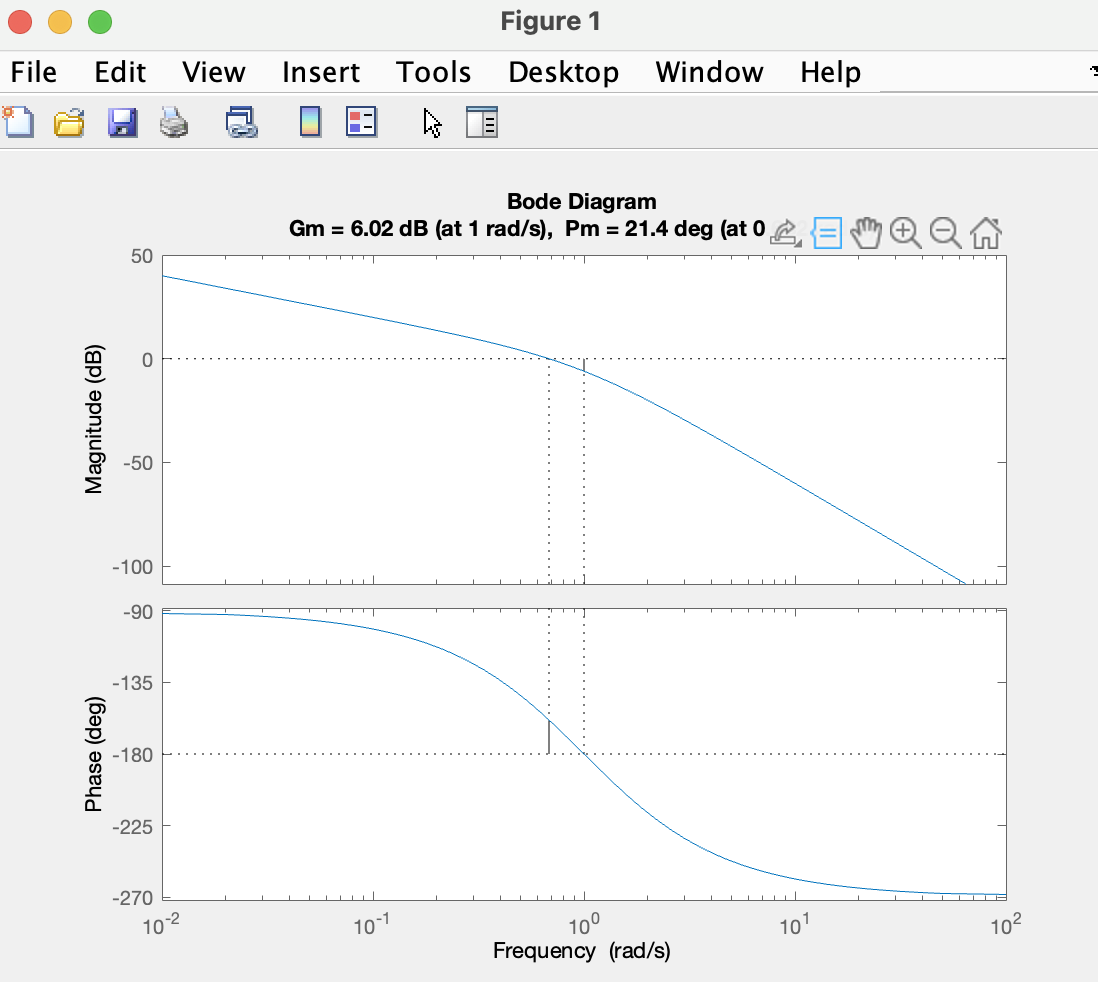
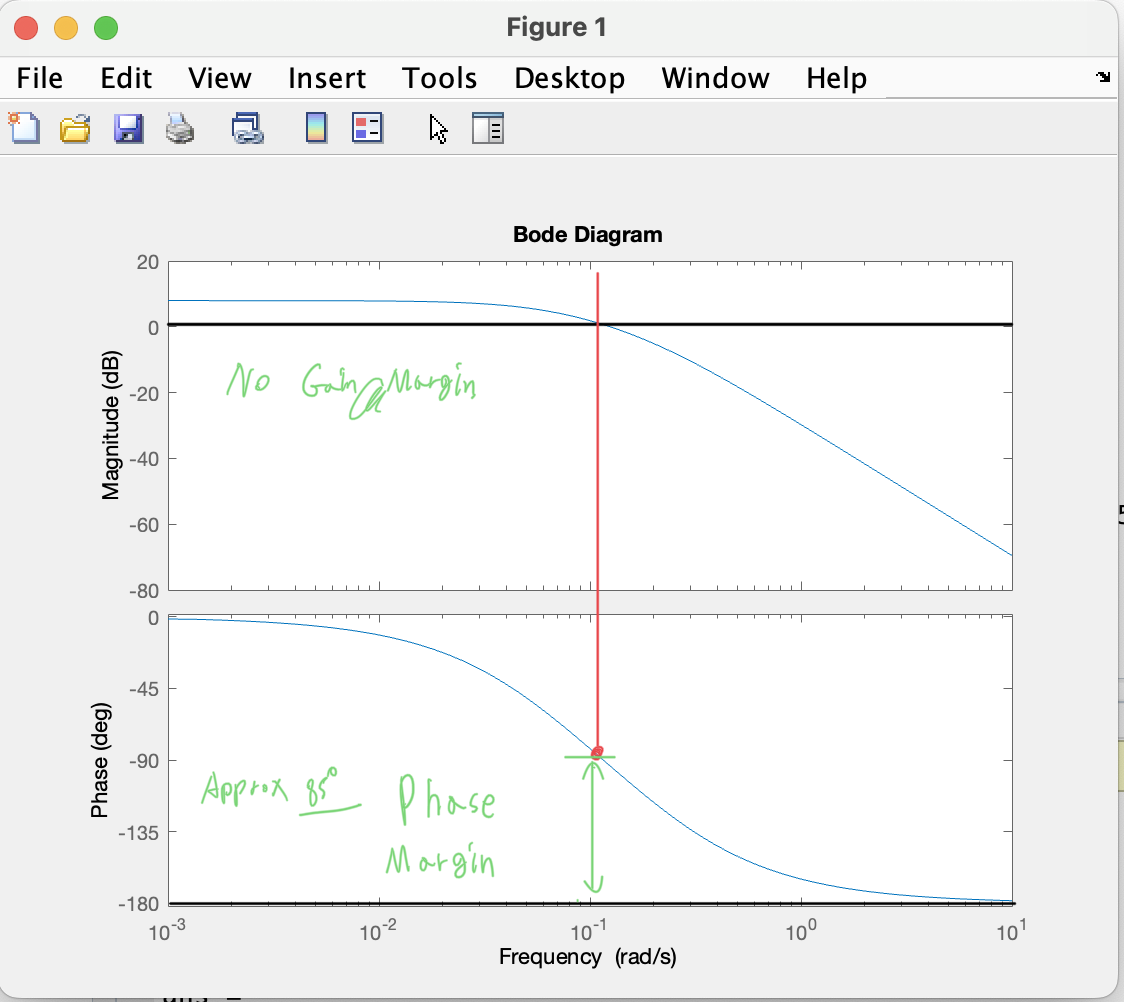
Phase Margin
위상 마진은 마진이 0 dB인 주파수에서 측정됩니다. 이를 일반적으로 "분할 주파수(Crossover frequency)"라고 합니다. 위상 마진는 측정된 위상에서 -180°의 위상 천이까지 거리를 측정한 값입니다. 즉, -180°에 도달하기 위해 위상이 얼마나 감소해야 하는지를 보여준다.
Gain Margin
게인 마진은 반면에 위상 천이가 -180°인 주파수에서 측정됩니다. 게인 마진은 측정된 게인부터 0dB의 게인까지 dB 단위로 측정된 거리를 나타냅니다. 0 dB 및 -180° 값이 충족되면 시스템이 불안정해지기 때문에 0dB 및 -180° 값이 중요하다
'제어공학 (Control Theory)' 카테고리의 다른 글
| 시스템 판별이란? (System Identification) (0) | 2022.11.29 |
|---|---|
| PID 제어기란? (0) | 2022.11.29 |
| 제어공학 간단 소개글 (0) | 2022.11.29 |
| 제어 시스템의 종류 (0) | 2020.05.02 |